7 Planar Graphs

A graph is a planar graph if it can be drawn in the plane with no edge crossings. [Note: You may need to rearrange the vertices to avoid crossings.]

7.1 Euler and Planarity

We have already seen that for planar graphs,

\[v - e + r = 1 + \mbox{number of connected components} \;,\] where \(v\) is the number of vertices, \(e\) the number of edges and \(r\) the number of regions.

In particular, for a connected graph we have \(v - e + r = 2\).

1. Show that the following are planar.
   1. \(K_{2,2}\)
   2. \(K_{2,3}\)
   3. \(K_{2,4}\)
   4. Is \(K_{2,n}\) planar for every \(n\)?

2. Use Euler’s formula to show that \(K_5\) is not planar. (Hint: how many regions would \(K_5\) have it if were planar? Why is that problematic?)

3. Use Euler’s formula to show that \(K_{3,3}\) is not planar.

7.2 Kuratowski’s Theorem

The proof of the following theorem is too involved for this course, but it turns out that all nonplanar graphs contain a “homeomorphic copy” of either \(K_{5}\) or \(K_{3,3}\).

Kuratowski’s Theoerm: A graph \(G\) is nonplanar if and only if it contains a subgraph \(H\) that is homeomorphic to either \(K_5\) or \(K_{3,3}\).

• two graphs are homeomorphic if the can be obtained from the same graph by a sequence of elementary subdivisions.

• an elementary subdivision of a graph \(G\) removes one edge \((u, v)\) and adds a new vertex \(n\) and two new edges \((u,n)\) and \((v,n)\).

4. Create a graph with 5 vertices and 7 edges. Now perform three elementary subdivisions on your graph.

5. Describe what an elementary subdivision is in siple words a kindergarterner could understand.

6. Explain why two homeomorphic graphs are either both planar or both nonplanar.

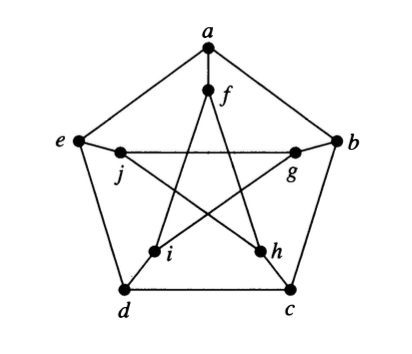
7. Use Kuratowski’s Theorem to show that the Petersen graph is nonplanar.