6 Bipartite Graphs

6.1 Definition

A simple graph \(G\) is biparatite if its vertices can be partitioned into two disjoint subsets \(V_1\) and \(V_2\) and every edge connects a vertex in \(V_1\) with a vertex in \(V_2\). The pair \(\langle<V_1, V_2\rangle\) is called a bipartition of \(G\).

6.2 Examples

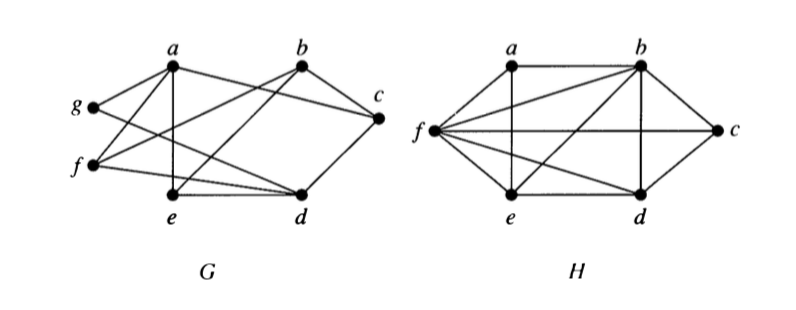
  1. Which of the following are bipartite?

  1. For what values of \(n\) are the following bipartite?
    1. \(K_n\)
    2. \(C_n\)
    3. \(Q_n\)

  2. Can a bipartite graph have more than one bipartition? If so, give an example. If not, explain why not.

  3. Describe an algorithm for checking whether a graph is bipartite. How efficient is your algorithm?

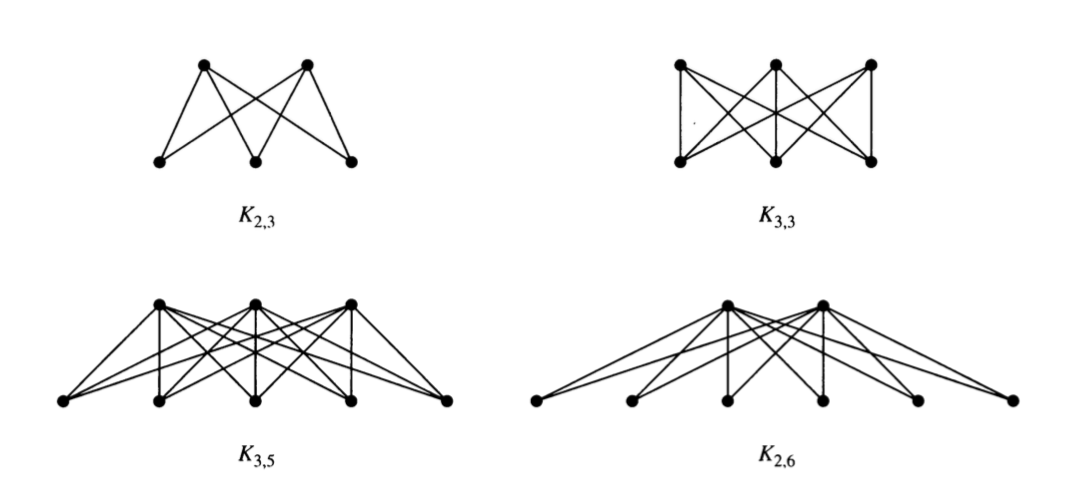
6.3 Complete Bipartite Graphs

A complete biparite graph \(K_{m,n}\) has two disjoint sets of vertices \(V_1\) and \(V_2\) with \(m\) and \(n\) elements. There is an edge between \(x\) and \(y\) if and only if \(x \in V_1\) and \(y \in V_2\) or \(x \in V_2\) and \(y \in V_1\).

Here are some examples.